数据结构 | Summer's blog

常见的数据结构包含哈希表(Hash Table)、队列(Queue)、栈(Stack)、链表(Linked List)、树(Tree)。下面进行详细介绍：

一、哈希表(Hash Table)

以伪代码举例：

a <- {
  '0' : 0,
  '1' : 2,
  '2' : 1,
  '3' : 56,
  '4' : 3,
  '5' : 67,
  '6' : 3,
  'length': 7
}

这个伪代码的形式可以看成是Hah模式，即key:value键值对的形式就可看作是Hash模式。例如Http请求和响应的第二部分数据就是Hash模式。数组也可以看成是hash模式。数组自带length属性。
如何使用hash呢？在计数排序中会用到。如：a <- [0,2,1,56,3,67,4,9,8]，在上一篇的博客中介绍的排序方式都需要进行比较，时间复杂度为NlogN。
此处使用计数排序来生成hash，数组a如上述代码块所定义，具体操作如下：

index <- 0
while (index < a['length'])
  number = a[index] //0,2,1,56,3,67,3
  if hash[number] == undefined
    hash[number] = 1
  else
    hash[number] = hash[number] + 1
  end
  index <- index + 1
end

根据以上代码生成的hash值为：

hash <- {
  '0' : 1,
  '2' : 1,
  '3' : 2,
  '56' : 1,
  '67' : 1
}

接下来我们按照顺序将生成的hash从小到大依次输出：

index2 <- 0
max <- findMax(a)
newArr <- []
while(index2 < max + 1)
  count = hash[index2]
  if count != undefined
    countIndex = 0
    while(countIndex < count)
      newArr.push(index2)
      countIndex <- countIndex + 1
  end
  index2 <- index2 + 1
end
print newArr

以上就是计数排序的伪代码。计数排序的时间复杂度O为n + max，比冒泡排序快很多。应用场景为对一个班级的人员年龄进行排序（此班级成员不都是同年）。这个排序方法存在两个缺点：

需要使用Hash作为计数排序的工具
无法对小数和负数进行排序

二、桶排序

桶排序和计数排序方法类似，区别在于计数排序一个桶里面之放置一个值，通排序里面的值在一个相同的取值范围内。以上个排序的数组为例，其生成的Hash值为：

hash <- {
  '0' : 1,
  '2' : 1,
  '3' : 2,
  '56' : 1,
  '67' : 1
}

木桶排序生成的Hash值为：

hash <- {
  '1' : [0,2,1,3,3],  // 0 - 10之间的数值
  '2': [],            // 10 - 20之间的数值
  '3': [],            // 20 - 30之间的数值
  '4': [],            // 30 - 40之间的数值
  '5': [],            // 40 - 50之间的数值
  '6': [56],          // 50 - 60之间的数值
  '7': [67]           // 60 - 70之间的数值
}

到此可以对比出计数排序使用的桶较多，木桶排序则较少，但是木桶排序需要在桶内进行二次排序。

三、基数排序

此处需要明确基数是什么。比如十进制的基数是10，我们使用的数字都是十进制，所以此排序中我们使用10作为基数进行排序。需要排序的数组为[23,202,103,566,32,617,37]。10作为基数的意思是一共存在10个桶，分别为0到9，我们将需要排序的数组首先进行个位对比，各位为0的放在第一个桶中（此桶为0），依次类推，所有数组按照个位数值大小入桶，然后使用数组连接将桶内数值做出桶处理。第二步再将得到的数组的十位进行对比，按照10位数值的大小依次入桶、出桶。最终能得到整个数组从小到大的排序。排序动画。

四、队列(Queue)

队列的特点：

先进先出
可以用数组实现
举例：排队

例子：

var q = [];
q.push('1');
q.push('2');
q.push('3');
//此时q队列中的顺序为['1','2','3']
q.shift()   //shift()为出队方法，出队的顺序是先进先出，所以此时出队的是'1'，返回'1'
q.shift()   //'2'出队，返回'2'

五、栈(Stack)

先进后出
可以用数组实现

日常中常见的例子就是坐电梯，假设先上去的人都是站在最里面，那么在出电梯的时候肯定是后上去的先出去，先上去的后出去这种方式，即先进后出。
例子：

var stack = [];
stack.push('1');
stack.push('2');
stack.push('3');
//此时q队列中的顺序为['1','2','3']
stack.pop()   //pop()为出栈方法，出栈的顺序是先进后出，所以此时出栈的是'3'，返回'3'
stack.pop()   //'2'出栈，返回'2'

六、链表

在数组中我们删除第一个元素或者最后一个元素都很好实现，可使用shift()/pop()删除首位/末尾。但是如果我们删除中间的某一个元素如删除下标为3的内容，那么需要将后面到数组元素依次往前提，这样做会非常麻烦。所以链表出现了。
链表的结构如图所示：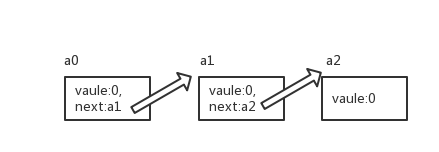

其中a0的值包含value，next值指向a1，a1的next指向a2。如果我们需要删除中间元素，如删除a1，我们只需要将a0的next指向a2，即a0.netx = a2。与此同时出现了新的问题，如果我们想访问到第n个元素的话，需要使用a0.next.next.next……next。这样操作非常的复杂。
综上，数组适用于查询快速只删除头尾的情况，链表适用于查询少但是需要从中间删除的情况。
链表中的两个概念：

head：链表中的第一个元素叫做head，如果没有head那么无法找到其他元素，如上图中的a0
node：链表中的每一个节点，即上图中的a0,a1,a2

七、树(Tree)

只要有层级结构就能够称之为树。浏览器打开的页面可以称之为树，页面中的DOM节点也可成为DOM树。
介绍几个概念：

层数：根元素所在的层为第1层或者第0层，由第1层扩展来的多个分支称为第二层，其他以此类推
深度：一共有多少层
节点个数：无子节点的节点称为叶子节点

二叉树
（从第0层开始）每个节点最多只有两个分之的树结构称为二叉树。二叉树的第i层至多拥有2^i个节点，总计拥有2^(i+1)-1个节点。

满二叉树
每一层的节点都是满的。

完全二叉树
在一棵二叉树中，除最后一层外，若其余层都是满的，并且最后一层或者是满的，或者是在最右边缺少连续若干节点，则此二叉树为完全二叉树。

完全二叉树和满二叉树可以用数组实现。如完全二叉树是从上到下从左到右依次存储在数组中的，如图所示：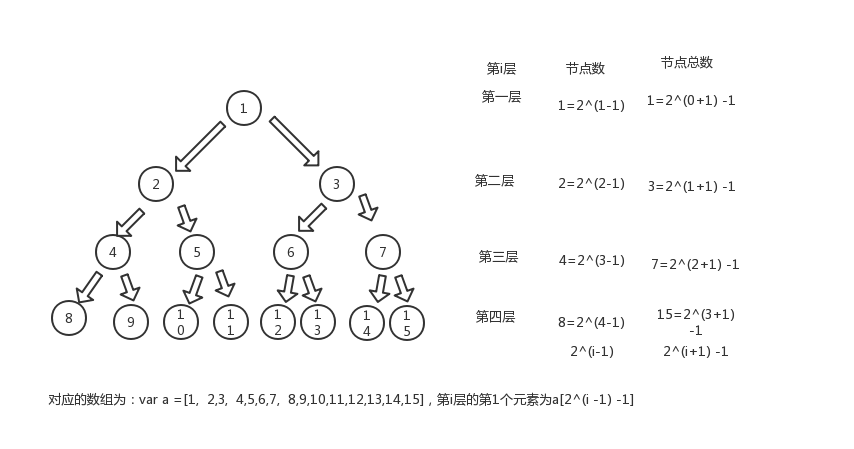
二叉树与数组

八、堆排序(Heap Sort)

堆是结构同于完全二叉树，有一点不同，堆的父节点的值永远大于子节点的值。
介绍两个概念：
最大堆：

最大堆中的最大元素值出现在根结点(堆顶)
堆中每个父节点的元素值都大于等于其孩子节点（如存在）

最小堆

最小堆中的最小元素值出现在根结点（堆顶）
堆中每个副节点的元素值都小于等于其孩子节点（如存在）

其他：B树、红黑树、AVL树。

—ç

附：计数排序伪代码

a <- { '0' : 2, '1' : 4, '2' : 6, '3' : 8, '4' : 2, '5' : 5,
'6' : 18, '7' : 57, '8' : 44, '9' : 8, 'length' : 10 }
hash <- {}
index <- 0
max <- a['0']
//将数组存入hash
while(index < a['length'])
  if a[index] == undefined
    hash[a[index]] <- 1
  else 
    hash[a[index]] <- hash[a[index]] + 1
  end
  if a[index] > max
    max <- a[index]
  end
  inex <- index + 1
end
//到此为止hash的值为：
//hash <- {'2' : 2, '4' : 1, '5' : 1, '6' : 1, '8' : 2, '18' : 1,
// '44' : 1, '57' : 1 }
index2 <- 0
newarr <- []
while(index2 <  max + 1)
  count <- hash[index2]
  if count != undefined
    index3 <- 0
    while(index3 < len)
      newarr.push(hash[index2])
      index3 <- index3 + 1
    end
  end
  index2 <- index2 + 1
end 
print newarr

个人原创，转载请注明出处。